Διάγραμμα Venn
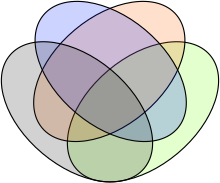
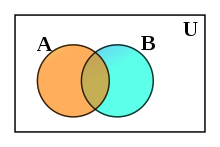
Το Διάγραμμα Venn είναι μια απεικόνιση συνόλων.
Σε κάθε διάγραμμα Venn υπάρχουν:
- ένα ορθογώνιο που συμβολίζει το μεγαλύτερο δυνατό σύνολο που μπορούμε να θεωρήσουμε, ανάλογα με το τί θέλουμε να δείξουμε και συμβολίζεται συνήθως με Ω ή U.
- Κλειστές γραμμές, συνήθως καμπύλες και κύκλοι, όπου η επιφάνεια που περικλείουν συμβολίζει το ίδιο το σύνολο.
Στο διάγραμμα Venn η κάθε επιφάνεια που ορίζεται από οποιοδήποτε συνδυασμό γραμμών συμβολίζει ένα σύνολο. Έτσι είναι λάθος να υπάρχει επιφάνεια που δεν αντιστοιχεί σε κάποιο σύνολο.
Μερικές φορές σε ένα διάγραμμα Venn συμβολίζονται μερικά στοιχεία συνόλων με κουκίδες, τα οποία μπορεί να συνοδεύονται από το αντίστοιχο σύμβολο του στοιχείου που απεικονίζουν.
Όλα τα στοιχεία ενός διαγράμματος Venn βρίσκονται μέσα στο ορθογώνιο.
Διαισθητική αντίληψη του διαγράμματος Venn
[επεξεργασία]Οι παρακάτω εικόνες δείχνουν με τις ομοιότητες και τις διαφορές των συνόλων αντικειμένων της καθημερινής ζωής. Τα διαγράμματα Venn είναι αφηρημένα σχήματα με σκοπό να απεικονίζουν οποιοδήποτε σύνολο οποιονδήποτε στοιχείων και να κατασκευάζονται σχετικά εύκολα με μολύβι και χαρτί.



