Σύστημα συντεταγμένων

Η σκακιέρα έχει ενσωματομένο ένα σύστημα συντεταγμένων. Χάρις αυτό μπορούν να καταγραφούν ολόκληρες διάσημες παρτίδες σκακιού χωρίς να χρειάζεται να κρατηθούν σε κάποια μορφή πολυμέσου.

Σύστημα συντεταγμένων ονομάζεται μια διαδικασία με την οποία κάθε διάνυσμα με αρχή ένα σημείο αναφοράς του χώρου ενδιαφέροντός μας προσδιορίζεται κατά μοναδικό τρόπο με μια διαδοχική σειρά αριθμών.

Ταμπέλες με κατευθύνσεις και νούμερα που προσδιορίζουν τη θέση. Παρατηρείστε ότι το σχήμα μιας τυπικής ταμπέλας είναι ένα βέλος όπως και το σύμβολο του διανύσματος. Σημαντική διαφορά μεταξύ των δύο είναι ότι το διάνυσμα έχει μήκος όσο το χαρακτηρίζει, ενώ η ταμπέλα που δείχνει 500m προς Heden δεν έχει μήκος 500 μέτρα!

Στην καθημερινή ζωή χρησιμοποιούνται αριθμοί για να περιγράψουν μια θέση, τοποθεσία ή κατεύθυνση. Για παράδειγμα οι εξής φράσεις:

• Ο φούρνος απέχει 5 μέτρα.
• Οι κάλτσες σου βρίσκονται στο τρίτο συρτάρι.
• Στρίψε στο τρίτο στενό.
• Το γραφείο του βρίσκεται στη διεύθυνση Πραξιτέλους 123, στο δέκατο όροφο, στην πόρτα 25.

Επιπλέον, συνήθως προσδιορίζεται κατεύθυνση.

• Ο φούρνος είναι στα δεξιά.
• Οι κάλτσες βρίσκονται στο κάτω συρτάρι.
• Γύρισε απ' την άλλη.
• Τα κλειδιά είναι μέσα στη τσάντα.

ή και τα δυο μαζί:

• Ο φούρνος είναι 5 μέτρα στα δεξιά.
• Οι κάλτσες βρίσκονται στο τρίτο συρτάρι από κάτω.
• Στρίψε στο τρίτο στενό δεξιά.
• Τα κλειδιά είναι μέσα στην κόκκινη τσάντα.

Ωστόσο, η έννοια του διανύσματος είναι πολύ συγκεκριμένη, δηλαδή προσδιορίζεται με αυστηρό τρόπο από αριθμούς και κατευθύνσεις.

Σημείο αναφοράς

Ο άνθρωπος ως σημείο αναφοράς.

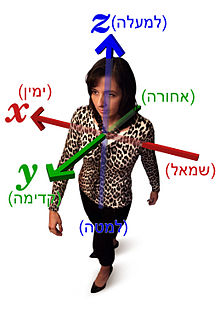
Στα συστήματα συντεταγμένων υπάρχει πάντα ένα σημείο αναφοράς ως προς το οποίο γίνεται ο προσδιορισμός. Στα παραπάνω παραδείγματα ο προσδιορισμός γίνεται ως προς το άτομο που ακούει τις οδηγίες, στο παράδειγμα με το φούρνο σύστημα αναφοράς είναι αυτός που δίνει τις οδηγίες.

Το σημείο αναφοράς θεωρείται ακίνητο και το διάνυσμα που αντιστοιχεί σε αυτό μέσω του συστήαματος συντεταγμένων είναι κατά κανόνα το μηδενικό διάνυσμα, δηλαδή το διάνυσμα του οποίου όλοι αριθμοί που το περιγράφουν ισούνται με μηδέν (στην καθημερινή ζωή συνήθως μπορεί να περιγραφθεί με τη λέξη εδώ).

Το σημείο αναφοράς είναι το σημείο εφαρμογής όλων των εφαρμοστών διανυσμάτων που προσδιορίζονται από το σύστημα στυντεταγμένων.

Στην παραπάνω εικόνα το σημείο αναφοράς είναι η διασταύρωση στην οποία ανήκει ή ο στύλος με τις ταμπέλες.

Επιπλέον το σημείο αναφοράς μπορεί να χρησιμοποιηθεί ως σημείο εφαρμοφής των ελεύθερων διανυσμάτων για την επισήμανση των μεταξύ τους σχέσεων. Τα αποτελέσματα γενικεύονται για το σύνολο των διανυσμάτων του ελεύθερου διανύσματος, αφού έχουν τα ίδια χαρακτηριστικά με οποιοδήποτε στοιχείο του.

Το σύστημα συντεταγμέων ως αλγεβρικό σώμα

Πλαγιογώνιο σύστημα αναφοράς τριών διαστάσεων. Κάθε σημείο του χώρου προσδιορίζεται επακριβώς από ένα γραμμικό συνδυασμό των τριών διανυσμάτων.

Το σύστημα συντεταγμένων είναι αλγεβρικό σώμα, γιατί ορίζεται πρόσθεση διανυσμάτων και βαθμωτός πολλαπλασιασμός. Έτσι, στον ν-διάστατο χώρο κάθε διάνυσμα μπορεί να προσδιοριστεί πλήρως ως γραμμικός συνδυασμός ν μη μηδενικών διανυσμάτων, δηλαδή αν στο τριδιάστατο χώρο γνωρίζουμε τρία διανύσματα${\vec {\alpha }},{\vec {\beta }},{\vec {\gamma }}$ που ανά δύο δεν έχουν την ίδια διεύθυνση, τότε κάθε διάνυσμα ${\vec {\delta }}$ γράφεται στη μορφή ${\vec {\delta }}=\kappa {\vec {\alpha }}+\lambda {\vec {\beta }}+\mu {\vec {\gamma }}$

Αντίστοιχη σχέση ισχύει και στο διδιάστατο και σε άλλον ν διάστατο χώρο. Αν θεωρήσουμε δεδομένα αυτά τα τρία διανύσματα (ή δύο διανύσματα για το επίπεδο), τότε κάθε διάνυσμα του συστήματος αναφοράς περιγράφεται κατά μοναδικό τρόπο από τρεις διατεταγμένους αριθμούς αριθμούς (δύο στην περίπτωση του επιπέδου) τους κ, λ, μ, και γράφουμε ${\vec {\delta }}=(\kappa ,\lambda ,\mu )$.

Οι αριθμοί που προσδιορίζουν κατά μοναδικό τρόπο κάθε διάνυσμα με αρχή το σημείο αναφοράς μέσω ενός συστήματος συντεταγμένων ονομάζονται συντεταγμένες.

Οι αριθμοί κ,λ,μ είναι οι συντεταγμένες του διανύσματος ${\vec {\delta }}$

Με αυτόν τον τρόπο προσδιορίστηκε πλήρως ένα σύστημα συντεταγμένων. Λοιπόν, κάθε σύστημα συντεταγμένων χρειάζονται να προσδιοριστούν το σημείο αναφοράς, και τόσα διανύσματα όσα και οι διαστάσεις του χώρου που περιγράφεται, υπό την προϋπόθεση ότι δεν έχουν ανά δύο την ίδια διεύθυνση. Με το σύστημα συντεταγμένων κάθε διάνυσμα του χώρου με αρχή το σημείο αναφοράς προσδιορίζεται από μια συγκεκριμένη διαδοχική ν-άδα αριθμών και αντίστροφα κάθε συγκεκριμένη ν-άδα αριθμών αντιστοιχεί ακριβώς σε ένα διάνυσμα με αρχή το σημείο αναφοράς.

Ανάλογα με τον τρόπο προσδιορισμού των συντεταγμένων υπάρχουν γενικά δύο συστήματα συντεταγμένων για το επίπεδο και τρία για τον τριδιάστατο χώρο στην αναλυτική γεωμετρία:

διδιάστατος χώρος (επίπεδο)

• Ορθοκανονικό σύστημα αναφοράς για το επίπεδο
• Πολικό σύστημα αναφοράς

τριδιάστατος χώρος

• Ορθοκανονικό σύστημα αναφοράς για τον τριδιάστατο χώρο
• Κυλινδρικό σύστημα αναφοράς
• Σφαιρικό σύστημα αναφοράς

Άξονες

Ένα σύστημα συντεταγμένων προσδιορίζεται πλήρως από έναν αριθμό μη συνευθειακών διανυσμάτων. Η προβολή ενός διανύσματος κατά τη διεύθυνση ενός τέτοιου διανύσματος είναι ένα διάνυσμα. Η σύγκριση του τρίτου ως προς το πρώτο διάνυσμα αποδίδει την αντίστοιχη συντεταγμένη. Κάθε διάνυσμα προσδιορίζεται από το σύστημα συντεταγμένων με την ανάλυση του σε συνιστώσες παράλληλες ως προς τα διανύσματα που χαρακτηρίζουν το σύστημα.

Οι χάρακες εδώ λειτουργούν ως άξονες σε μια περιοχή του επιπέδου.

Απλό σύστημα αναφοράς ενός άξονα. Κάθε σημείο αντιστοιχεί σε έναν αριθμό.

Πλαγιογώνιο επίπεδο σύστημα συντεταγμέων. Η προβολές του διανύσματος που χρησιμοποιούνται είναι αυτές που είναι παράλληλες στους άξονες.

Αν ένας "χάρακας" τοποθετούνταν έτσι, ώστε το μηδέν του να είναι το σύστημα αναφοράς και το 1 το αρχικό διάνυσμα, τότε η συνιστώσα θα έδειχνε στο χάρακα την τιμή της συντεταγμένης στην οποία αντιστοιχεί. Επειδή η συνιστώσα μπορεί να είναι αντίθετη από το αρχικό διάνυσμα, ο νοητός χάρακας έχει αρνητικές τιμές προς αυτήν την κατεύθυνση.

Τη λειτουργία αυτού του χάρακα αναλαμβάνει ο άξονας.

Άξονας είναι μια προσανατολισμένη ευθεία κατά την κατεύθυνση ενός από τα διανύσματα του συστήματος συντεταγμένων, βαθμωνομημένη, έτσι ώστε να έχει το μηδέν στο σημείο αναφοράς και το ένα στο πέρας του διανύσματος.

Τα θετικά νούμερα βρίσκονται κατά την κατεύθυνση που δείχνει το αντίστοιχο διάνυσμα του συστήματος και τα αρνητικά στην άλλη. Αυτό το αντίστοιχο διάνυσμα του συστήματος ονομάζεται μοναδιαίο διάνυσμα.

Έστω ότι δύο διανύσματα βρίσκονται πάνω σε έναν άξονα. Τότε η συντεταγμένη του αθροίσματός δύο διανυσμάτων είναι το αλγεβρικό άθροισμα των συντεταγμένων των δύο αρχικών διανυσμάτων, τα οποία είναι η συνιστώσες της συνισταμένης.

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Διανυσματική σχέση	Εξήγηση
${\vec {\alpha }}+{\vec {\beta }}={\vec {\gamma }}$	Έστω ${\vec {\alpha }},{\vec {\beta }}$ τα δύο διανύσματα και ${\vec {\gamma }}$ το άθροισμά τους.
${\vec {\alpha }}=\kappa {\vec {i}},{\vec {\beta }}=\lambda {\vec {i}},{\vec {\gamma }}=\mu {\vec {i}}$	Τα τρία διανύσματα έχουν συντεταγμένες κ,λ,μ στον άξονα με μοναδιαίο διάνυσμα το ${\vec {i}}$.
$\Rightarrow \kappa {\vec {i}}+\lambda {\vec {i}}=\mu {\vec {i}}$	Αντικατάσταση στην πρώτη σχέση με τις δεύτερες.
$\Rightarrow (\kappa +\lambda ){\vec {i}}=\mu {\vec {i}}$	Επιμεριστική ιδιότητα του βαθμωτού πολλαπλασιασμού των διανυσμάτων.
$\Rightarrow \kappa +\lambda =\mu$	Επειδή το διάνυσμα ${\vec {i}}$ δεν είναι μηδενικό προκύπτει αυτή η σχέση που είναι και το ζητούμενο.

Πρέπει να τονιστεί ότι οι προβολές πάνω σε έναν άξονα δεν είναι πάντα ορθές, αλλά εξαρτώνται από το ίδιο το σύστημα αναφοράς. Συνήθως γίνονται υπό την γωνία των μοναδιαίων διανυσμάτων.

Συντεταγμένες

Το πέρας κάθε συνισταμένης αντιστοιχεί σε ένα σημείο του αντίστοιχου άξονα, το οποίο με τη σειρά του αντιστοιχεί σε έναν πραγματικό αριθμό, αυτόν που προσδιορίζει την αντίστοιχη συντεταγμένη.

Αν ο άξονας είναι ένας, τότε η συντεταγμένη ονομάζεται τετμημένη. Αν οι άξονες είναι δύο, τότε μία συντεταγμένη ονομάζεται τετμημένη και η άλλη τεταγμένη. Στην αναγραφή ενός διανύσματος στη μορφή (α,β) ο αριθμός α είναι η τετμημένη και ο αριθμός β η τεταγμένη.

Ορθοκανονικό σύστημα αναφοράς

Ορθοκανονικό σύστημα αναφοράς Οxyz με έναν παρατηρητή.

Ορθοκανονικό σύστημα συντεταγμένω. Η τετμημένη του διανύσματος είναι το 2 και η τεταγμένη το 3.

Αν τα μοναδιαία διανύσματα του συστήματος είναι κάθετα μεταξύ τους, τότε το σύστημα ονομάζεται ορθογώνιο, αλλιώς ονομάζεται πλαγιογώνιο. Αν τα μοναδιαία διανύσματα ενός ορθογώνιου συστήματος συντεταγμένων έχουν μήκος ίσο με 1 (άρα τα μήκη όλων των διανυσμάτων είναι ίσα μεταξύ τους) και διατάσσονται δεξιόστροφα, τότε ονομάζεται ορθοκανονικό ή καρτεσιανό σύστημα συντεταγμένων. Συνήθως το επίπεδο ορθοκανονικό σύστημα αναφοράς συμβολίζεται με Οxy και το τριδιάστατο Oxyz. Κάθε διάνυσμα ${\vec {\delta }}$ αυτού του συστήματος γράφεται στη μορφή (x,y,z), δηλαδή ${\vec {\delta }}=x{\vec {i}}+y{\vec {j}}+z{\vec {k}}$. Ένα σύστημα αναφοράς είναι καρτεσιανό αν και μόνο αν για τα τρία μοναδιαία διανύσματα ${\vec {i}},{\vec {j}},{\vec {k}}$ ισχύουν:

${\vec {i}}\times {\vec {j}}={\vec {k}},{\vec {j}}\times {\vec {k}}={\vec {i}},{\vec {k}}\times {\vec {i}}={\vec {j}}$

${\vec {i}}\cdot {\vec {j}}={\vec {j}}\cdot {\vec {k}}={\vec {k}}\cdot {\vec {i}}=0$

Άσκηση: Αποδείξτε ότι οι παραπάνω σχέσεις ισχύουν αν και μόνο αν το σύστημα συντεταγμένων είναι καρτεσιανό.
σχήμα	Ευθύ	Αντίστροφο
	Οι πρώτες τρεις σχέσεις σημαίνουν ότι το σύστημα είναι δεξιόστροφο, η τελευταία ότι τα μοναδιαία διανύσματα είναι κάθετα μεταξύ τους. Επειδή τα διανύσματα είναι κάθετα μεταξύ τους οι τρεις πρώτες σχέσεις μπορούν να γίνουν μετρικές $|{\vec {i}}|\cdot |{\vec {j}}|=|{\vec {k}}|,|{\vec {j}}|\cdot |{\vec {k}}|=|{\vec {i}}|,|{\vec {k}}|\cdot |{\vec {i}}|=|{\vec {j}}|$ το οποίο σύστημα των τριών εξισώσεων έχει μοναδική λύση $|{\vec {i}}|=|{\vec {j}}|=|{\vec {k}}|=1$. Έτσι, τα τρία μοναδιαία διανύσματα έχουν μήκος ίσο με 1, είναι κάθετα ανά δύο και το σύστημα είναι δεξιόστροφο, άρα είναι καρτεσιανό.	Η τελευταία σχέση προκύπτει γιατί τα διανύσματα είναι κάθετα. Επιπλέον, επειδή είναι κάθετα ισχύει και η σχέση ${\vec {i}}\times {\vec {j}}=\lambda {\vec {k}}$. Μπορεί να γίνει μετρική ως $|{\vec {i}}|\cdot |{\vec {j}}|=|{\vec {k}}|$ και επειδή τα διανύσματα έχουν μήκος ένα ισχύει λ=1, άρα ${\vec {i}}\times {\vec {j}}={\vec {k}}$. Παρομοίως ισχύουν και οι ${\vec {j}}\times {\vec {k}}={\vec {i}},{\vec {k}}\times {\vec {i}}={\vec {j}}$

Πολικό σύστημα συντεταγμένων

Πολικό σύστημα συντεταγμένων.

Το πολικό σύστημα συντεταγμένων είναι επίπεδο και προσδιορίζει τα διανύσματα με αρχή το σημείο αναφοράς του επιπέδου με βάση δύο παραμέτρους:

• Την απόστασή τους από το σημείο αναφοράς.
• Την κατεύθυνσή τους σε σχέση με τον άξονα x'x και y'y, αν το σύστημα ήταν ορθογώνιο.

Οι συντεταγμένες είναι δύο θετικοί πραγματικοί αριθμοί, το μήκος του διανύσματος ρ και η γωνία θ που σχηματίζει κατά τη θετική φορά με τον ημιάξονα Οx. Οι πολικές συντεταγμένες συνδέονται με τις καρτεσιανές με τις εξής σχέσεις:

• $x=\rho cos\theta$
• $y=\rho sin\theta$

Ερωτήσεις

Σύστημα συντεταγμένων σε λουκουμά όπου προσδιορίζονται οι δύο άξονες. Το σύστημα συντετεγμένων που θα χρησιμοποιηθεί εξαρτάται από τη γεωμετρία του χώρου, όπου εδω είναι η επιφάνεια ενός λουκουμά.

• Τί είναι οι συντεταγμένες;
• Ένα διάνυσμα εξαρτάται από το σύστημα συντεταγμένων που χρησιμοποιούμε. Σωστό ή λάθος;
• Κάθε διάνυσμα ενός χώρου μπορεί να προσδιοριστεί επακριβώς από ένα σύστημα συντεταγμένων. Σωστό ή λάθος;
• Ποιές γεωμετρικές έννοιες αναπαριστούν οι σχέσεις των αρχικών διανυσμάτων του καρτεσιανού συστήαμτος αναφοράς;

Καρτεσιανό σύστημα συντεταγμένων

• • Ποιό είναι το σημείο αναφοράς; Αφού το εντοπίσετε θεωρείστε ότι ονομάζεται Ο.
  • Τί είδους σύστημα συντεταγμένων είναι; Πόσων διαστάσεων είναι και πώς συμβολίζεται;
  • Ποιοί είναι οι άξονες; Ποιός είναι ο άξονας των τεταγμένων και ποιός ο άξονας των τετμημένων;
  • Ποιά είναι η θετική φορά σε κάθε άξονα και ποιά η αρνητική;
  • Τοποθετήστε όλα τα διανύσματα με αρχή το σημείο αναφοράς (νοητά ή ξανακατασκευάστε το σχήμα). Ποιό διάνυσμα αναλύεται και σε ποιά διανύσματα; Τί σχέση έχουν όλα αυτά μεταξύ τους;
  • Υπολογίστε σε αυτό το σύστημα τις συντεταγμένες των διανυσμάτων:
    • (α,β)+(γ,δ)
    • (α,β)-(γ,δ)
    • (α,β)$\cdot$(γ,δ)
    • (α,β)$\times$(γ,δ)
    • Σε ποιό σύστημα αναφοράς είναι το αποτέλεσμα της τελευταίας πράξης;
    • Υπολογίστε τα αντίστοιχα στο τριδιάστατο ορθοκανονικό σύστημα αναφοράς.

Απαντήσεις στην παραπάνω ομάδα ερωτήσεων
Σημείο αναφοράς είναι το σημείο τομής των αξόνων, εκεί μηδενίζονται οι τιμές τους.
Το σύστημα συντεταγμένων είναι διδιάστατο ορθοκανονικό σύστημα συντεταγμένων και συμβολίζεται με Οxy.
Οι άξονες είναι οι δύο επισημασμένες βαθμονομημένες ευθείες. Ο οριζόντιος είναι ο άξονας x'x και ο άξονας των τετμημένων, ενώ ο κάθετος είναι ο άξονας y'y και ο άξονας των τεταγμένων.
Στον άξονα x'x η θετική φορά είναι προς τα δεξιά, ενώ στον y'y προς τα πάνω.
Το πλάγιο διάνυσμα αναλύεται στα δύο διακεκομμένα κάθετα. Η συνιστώσα είναι το άθροισμα των συνιστωσών.
(α,β)+(γ,δ)=(α,0)+(0,β)+(γ,0)+(0,δ)=(α+γ,0)+(0,β+δ)=(α+γ,β+δ)
(α,β)-(γ,δ)=(α,0)+(0,β)-(γ,0)-(0,δ)=(α,0)+(0,β)+(-γ,0)+(0,-δ)=(α-γ,β-δ)
(α,β)$\cdot$(γ,δ)=(α,0)$\cdot$((γ,0)+(0,δ))+(0,β)$\cdot$((γ,0)+(0,δ))=(α,0)$\cdot$(γ,0)+(α,0)$\cdot$(0,δ)+(0,b)$\cdot$(γ,0)+(0,b)$\cdot$(0,δ)=αγ+βδ
(α,β)$\times$(γ,δ)=(α,0)$\times$((γ,0)+(0,δ))+(0,β)$\times$((γ,0)+(0,δ))=(α,0)$\times$(γ,0)+(α,0)$\times$(0,δ)+(0,b)$\times$(γ,0)+(0,b)$\times$(0,δ)= =$|$α$||$δ$|$ημ(α,δ)${\hat {k}}$+$|$β$||$γ$|$ημ(β,γ)${\hat {k}}$=(αδ-βγ)${\hat {k}}$=${\begin{vmatrix}\alpha &\beta \\\gamma &\delta \end{vmatrix}}$${\hat {k}}$
Η τελευταία πράξη δίνει αποτέλεσμα στο σύστημα Oxyz.
(α,β,γ)+(δ,ε,ζ)=(α+δ,β+ε,γ+ζ), (α,β,γ)$\cdot$(δ,ε,ζ)=αδ+βε+γζ, (α,β,γ)$\times$(δ,ε,ζ)=${\begin{vmatrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\\alpha &\beta &\gamma \\\delta &\epsilon &\zeta \end{vmatrix}}$ με άνοιγμα υποχρεωτικά ως προς την πρώτη σειρά

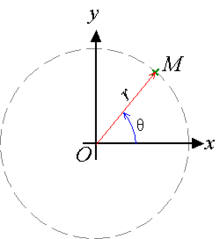
Πολικό σύστημα συντεταγμέων

• Οι πολικές συντεταγμένες ενός διανύσματος είναι ρ=9 και θ=π. Ποιό είναι το μήκος του διανύσματος;
• Γιατί ισχύουν οι σχέσεις μεταξύ πολικού και καρτεσιανού συστήματος συντεταγμένων;
• Εκφράστε το διάνυσμα ρ=10, θ=π/3 σε καρτεσιανές συντεταγμένες στο ίδιο επίπεδο.
• Υπάρχουν σχέσεις που να μετατρέπουν τις πολικές συντεταγμένες σε καρτεσιανές;
• Δεδομένου ότι το πολικό σύστημα συντεταγμένων συνδέεται με τον κύκλο και ότι ένας άξονας είναι ευθεία, πώς θα προσδιορίζονται οι κυλινδρικές συντεταγμένες;
• Πώς προσδιορίζονται οι σφαιρικές συντεταγμένες;